I’ve often thought there must be an easy way to relate the bandwidth of a power-supply control loop to its transient response, but never really found a good reference that defined this in simple terms. It seems like a straightforward problem, which should have a simple solution. The higher the bandwidth, the faster the loop responds, and with less voltage deviation.
Several limiting factors may get in the way of this simple relationship. First is the series resistance of the output capacitor. If the resistance is too high, then the load step creates a large voltage deviation before the control loop can respond. Equation 1 gives the peak voltage deviation:
Second, the inductor can cause slew-rate limiting. This is related to the control-loop bandwidth by the voltage across the inductor, calculated with Equation 2:
Third, there is a critical inductance limit beyond which the duty cycle will saturate. The peak transient voltage is then determined by the large-signal limiting of the inductor current into the output capacitor. This is related to the voltage across the inductor, output capacitor and series resistance, expressed by Equation 3:
Let’s say you design your power supply to avoid these issues and use an electronic load to test the transient response. If your control-loop bandwidth is relatively high, you may find that the output voltage follows the load current and is not limited by the control loop. In this case, you can use a MOSFET and load resistor on a small board for the load step, controlled by a function generator. A low duty cycle for the load on-time will minimize dissipation in the resistor. It is important to mount this as close to the power-supply output as possible in order to minimize wiring inductance. Figure 1 shows a typical setup. The small black wire connects to a surface-mount coax for the output voltage measurement.

Figure 1: Typical power-supply test setup for fast load transient
Figure 2 shows the measured transient response, which is directly related to the bandwidth of the control loop in Figure 3. With no equivalent series resistance (ESR), slew rate or duty-cycle limiting, the initial response time is one-fourth the effective control-loop period. This is the equivalent first quarter of a sinusoidal response at the unity-gain frequency. The peak voltage will vary based on the topology and damping, but is easily predictable with a surprising degree of accuracy.

Figure 2: The measured transient response shows tP = 25μs and VP = 130mV for a load step of ∆I = 5A
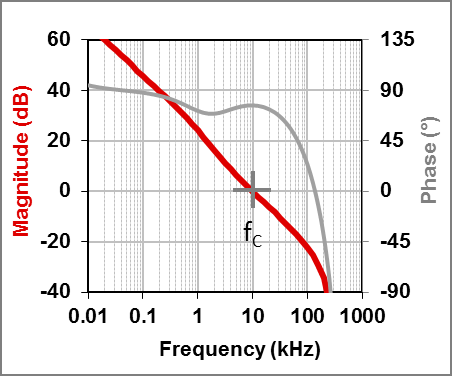
Figure 3: The corresponding control-loop bandwidth is 10kHz
With no ESR, slew rate or duty-cycle limiting, Equation 4 calculates tP as:
For current-mode control, Equation 5 gives the single-pole approximation that results in the peak voltage deviation:
Equation 6 calculates the critically damped case for current-mode control (as shown in Figure 2):
For voltage-mode control, Equation 7 gives the peak voltage deviation:
It is important to verify the performance over all operating conditions. Duty-cycle limiting can cause a significant droop when operating the control loop outside its linear range, as shown in Figure 4.

Figure 4: Comparison of output voltage with different input voltages at a 5A load step
As you can see the relationship between bandwidth and transient response is simple and straightforward. By observing the transient response you can quickly get a good estimate of the control loop bandwidth.
Additional resources
- The 2014 Applied Power Electronics Conference and Exhibition paper “Frequency Compensation and Power Stage Design for Buck Converters to Meet Load Transient Specifications” has more information about this topic, including design methods to meet transient response.